Motivation
I saw someone illustrating his/her solution with a “superior triangle”.
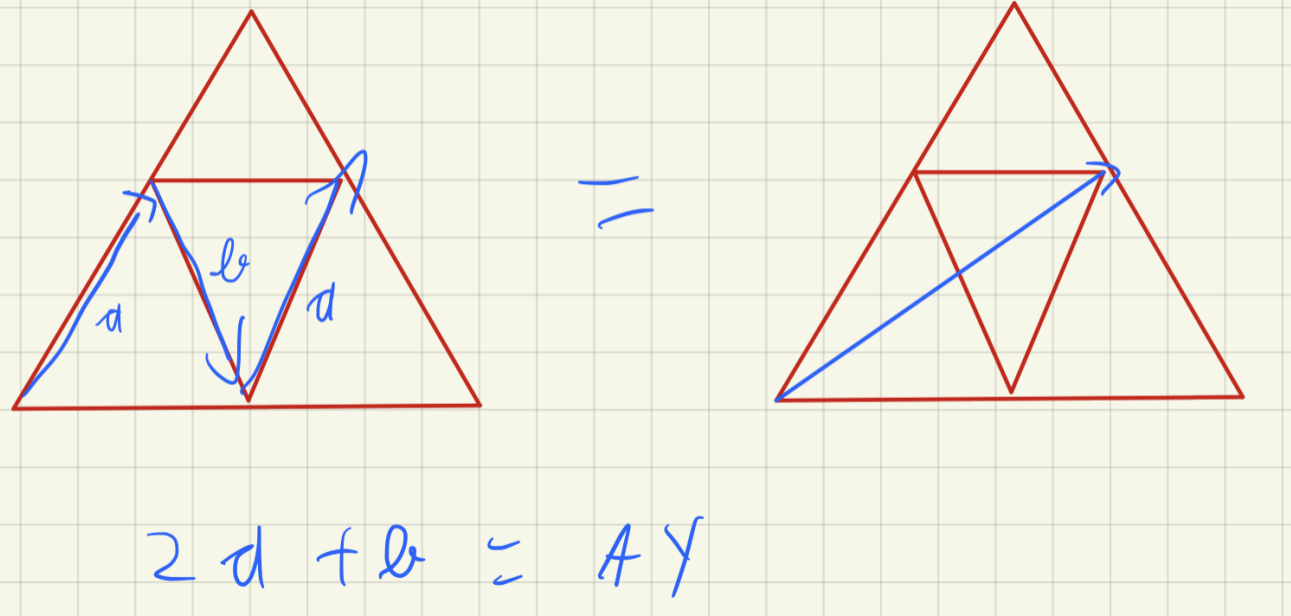
This reminds me the homothety about the centroid of factor −1/2.
The above picture \usetikzlibrary{calc} for computing coordinates from those
of existing points. (A)!.25!(B) means $(A)+.25[(B)-(A)]$.
\begin{tikzpicture}[scale=2]
\coordinate (D) at (-0.7,1);
\coordinate (E) at (-1,0);
\coordinate (F) at (1,0);
\coordinate (A) at ($(E)!.5!(F)$);
\coordinate (B) at ($(F)!.5!(D)$);
\coordinate (C) at ($(D)!.5!(E)$);
\coordinate (G) at ($(D)!.5!(E)!1/3!(F)$);
\draw (A) -- (B) -- (C) -- cycle;
\draw (D) -- (E) -- (F) -- cycle;
\begin{scriptsize}
\fill (G) circle (0.5pt) node [left=2pt,anchor=north]{$G$};
\end{scriptsize}
\draw[->,-latex,dashed] (D) -- (A);
\draw[->,-latex,dashed] (E) -- (B);
\draw[->,-latex,dashed] (F) -- (C);
\end{tikzpicture}
Previous post
From the homothety between the nine-point circle and circumcircle about orthocenter with a factor of 2, we see that the nine-point center is the mid-point of orthocenter and circumcenter.
It’s possible to make use of the conclusion that AH = 2OMA to see that △AH? ∼ △MAO?. Then we use the well-known property that AG:GMA = 2:1 to see that ? = G.
Easier way to put centroid onto Euler line
orthocenter of smaller △ (H) = circumcenter of larger △
circumcenter of larger △ → circumcenter of smaller △ (O) under h(G, −1/2)
The factor is negative because the arrows pass through the center of homothety G to another side.
From this homothety, we see that G, H and O are collinear, and HG:GO = 2:1.
My sample illustration
The above diagram was first drawn on Geogebra web app, then converted to LaTeX code using the method in TikZ templates. After that, I cleaned the code so that the numbers below have at most two decimal places, and manually adjusted some label texts and positions.
\documentclass[tikz]{standalone}
\begin{document}
\definecolor{dqfqcq}{rgb}{0.8,0.95,0.75}
\definecolor{ffzzff}{rgb}{1,0.6,1}
\definecolor{ffxfqq}{rgb}{1,0.5,0}
\definecolor{qqzzcc}{rgb}{0,0.6,0.8}
\begin{tikzpicture}
\clip(-3.5,-6) rectangle (5.5,0.5);
\fill[line width=0.8pt,fill=dqfqcq,fill opacity=1] (3,0) -- (5,-5) -- (-3,-5) -- cycle;
\draw [line width=1.2pt] (3,0)-- (5,-5);
\draw [line width=1.2pt] (5,-5) -- (-3,-5);
\draw [line width=1.2pt] (-3,-5)-- (3,0);
\draw [line width=1.2pt,domain=-4:6.5,dashed,opacity=0.5] plot(\x,{(-4.25+0.55*\x)});
\draw (3.5,-0.75) node[anchor=north west] {$\overline{HA} = 2.6$};
\draw [line width=1.2pt] (3,0)-- (3,-2.6);
\draw [line width=1.2pt] (1,-3.7) -- (1,-5);
\draw [line width=1.2pt] (3,0)-- (1,-5);
\draw (1.4,-4.2) node[anchor=north west] {$\overline{OM_A} = 1.3$};
\draw (3,0.2) node {$A$};
\draw (5.2,-5) node {$B$};
\draw (-3.2,-5) node {$C$};
\draw [fill=qqzzcc] (1.67,-3.33) circle (2.5pt);
\draw[color=qqzzcc] (1.6,-3) node {$G$};
\draw [fill=ffxfqq] (1,-3.7) circle (2.5pt);
\draw[color=ffxfqq] (1.1,-3.4) node {$O$};
\draw [fill=ffzzff] (3,-2.6) circle (2.5pt);
\draw[color=ffzzff] (3.2,-2.2) node {$H$};
\draw [fill=black] (1,-5) circle (1.5pt);
\draw (1.2,-5.3) node {$M_A$};
\end{tikzpicture}
\end{document}