Motivation
Someone on Discord asked about the existence of the nine-point circle. It’s well-known that that can be proved by homothety.
Little reminder about homothety
Homothety preserves angles (and thus parallel lines). Homothetic polygons are similar, so the ratio of the corresponding sides is the same. Considering the radii of a circle under a homothety, we see that a homothety maps a circle to another circle.
Notation
- H: orthocenter
- G: centroid
- O: circumcenter
- ω: circumcircle
- HA: feet of altitude with respect to A.
- MA: midpoint of side a.
- EA: Euler point with respect to A. (i.e. midpoint of A and H)
Problem
The second proof for nine-point circle on AoPS starts with a proved fact that the reflection of H about a and MA lie on ω.
The first part is easy. I changed the definition of HA’ from “reflect(H, a)” to “AH ∩ ω”.
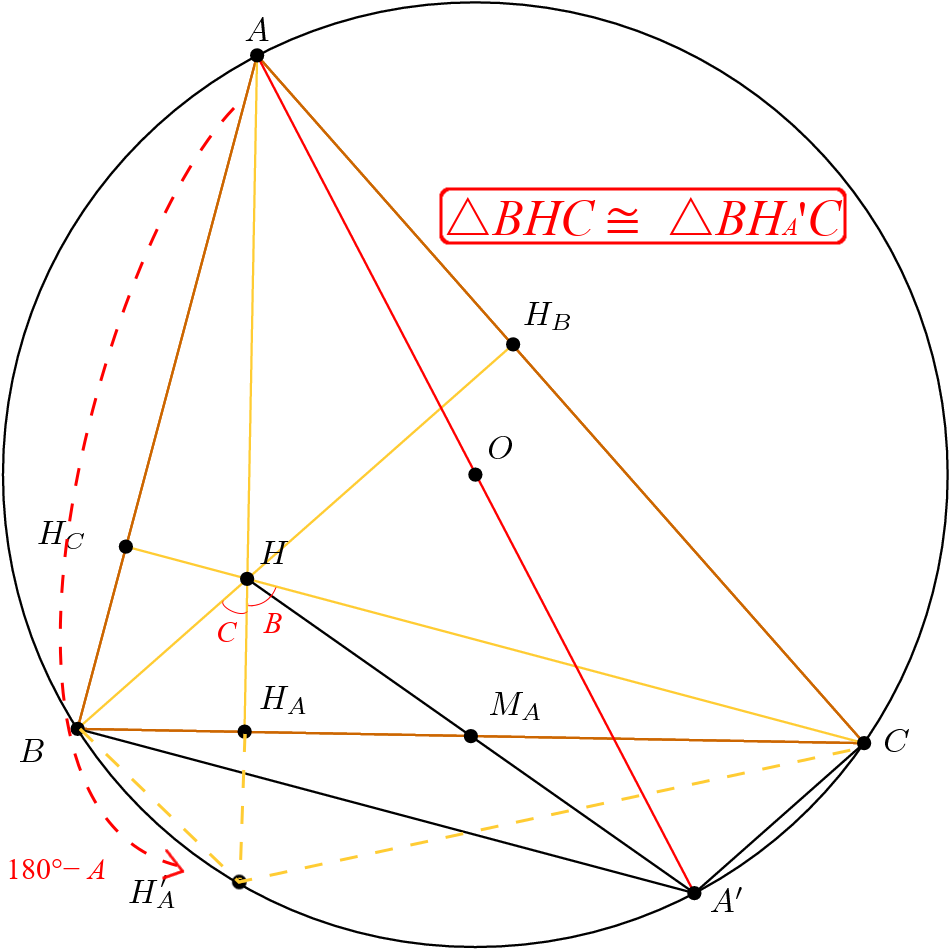
In either definition, we can prove △BHC ≅ △BHAC. In my definition, use ∠CBHA’ = ∠CAH = ∠CBH = 90° − C.
I found the second part is harder because I used A’ := HMA ∩ ω" instead of “reflect(H, MA)”. After thinking about that for hours, I gave up and searched for “nine point circle homothety” for answer, but the information was too advanced for me. Finally, I searched with more relevant keywords “orthocenter reflection”, and I found the hints from this relevant Math.SE question.
Solution 1
In the linked solution on Math.SE, A’ := reflect(H, MA). It’s easy to see that BA’CH is a parallelogram, so ∠BA’C = ∠BHC = B + C = 180° − A. As a result, A’ ∈ ω.
Solution 2
Using my definition of A’, just reverse the reasoning above.
We see that A’C ⟂ AC and A, A’, C ∈ ω, so AA’ is a diameter for ω. This shows that AH = 2OMA.
Solution 3
On this post on AoPS, A’ := reflect(A, O).
Corollary
The nine-point circle is the image of the circumcircle ω under the homothety h(H, 1/2).